Question

1. An object moves along a straight path whise distance from the reference point is given by the position function, d(t) =t²+4t+12m after t seconds. Find: a. The position of the object after 1,2,3,4 and 5 seconds.b. The average velocity of the object from 3 seconds to 4 secondsc. The displacement from 1 second to 2 seconds.d. The instantaneous velocity after 3 seconds and after 5 seconds.e. The accelaration at t second/s.

Answer 1

Answer:

a) 17m, 24m, 33m, 44m, 57m

b) 7 m/s

c) 7m

d) 10m/s; 14m/s

e) 8

Step-by-step explanation:

Given:

d(t) = t² + 4t + 12 m

To find:

a. The position of the object after 1,2,3,4 and 5 seconds.

b. The average velocity of the object from 3 seconds to 4 seconds

c. The displacement from 1 second to 2 seconds.

d. The instantaneous velocity after 3 seconds and after 5 seconds.

e. The acceleration at t second/s.​

a) To get the position after 1, 2, 3, 4, and 5 seconds, we will substitute t for 1, 2, 3, 4, and 5 respectively. This is because d(t) represents the postion at t seconds

d(1) = (1)² + 4(1) + 12 = 1 + 4 + 12 = 17m

d(2) = (2)² + 4(2) + 12 = 4 + 8 + 12 = 24m

d(3) = (3)² + 4(3) + 12 = 9 + 12 + 12 = 33m

d(4) = 4² + 4(4) + 12 = 44m

d(5) = 5² + 4(5)+ 12 = 57m

b) To get the average velocity of the object from 3 to 4 seconds, we will apply the formula:

`\begin{gathered} average\text{ velocity = }\frac{change\text{ in position}}{change\text{ in time}} \\ average\text{ velocity = }\frac{d(2)\text{ - d\lparen1\rparen}}{2\text{ - 1}}\text{ = }\frac{24\text{ - 17}}{2-1}\text{ = }(7)/(1) \\ average\text{ velocity = 7 m/s} \end{gathered}`

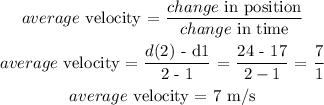
c) The displacement at 1 and 2 seconds respectively will be the difference of the positions at this time

d(2) = 24 m, d(1) = 17 m

displacement = d(2) - d(1) = 24 - 17

displacement = 7m

d) To get the instantaneous velocity, we need to first differentiate with respect to t.

`\begin{gathered} (d(d))/(dt)\text{ = }(d(t²+4t+12))/(dt) \\ (d(d))/(dt)=\text{ 2t + 4} \\ (dv)/(dt)=(d(d))/(dt) \\ (dv)/(dt)=2t\text{ + 4} \end{gathered}`

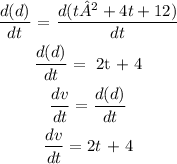
Then we will substitute t for 3 and 5 respectively.

dv/dt at t = 3 secs

dv/dt = 2(3) + 4 = 10 m/s

dv/dt at t = 5 secs

dv/dt = 2(5) + 4 = 14 m/s

e) To get acceleration, we will differentiate the function for the position with respect to t twice.

We did the first differential in instantenously velocity. We will differentiate the result again to get the acceleration with respect to t

`\begin{gathered} d\left(t\right)=t²+4t+12 \\ (dv)/(dt)=\text{ 2t + 4} \\ (da)/(dt)\text{ = }(d(dv\rparen)/(dt)=\text{ }\frac{d(2t\text{ + 4\rparen}}{dt} \\ \\ (da)/(dt)\text{ = 2} \end{gathered}`

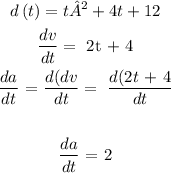
The value of our acceleration at t seconds is a constant. This means the acceleration will be constant throughout

Hence, the acceleration at t seconds = 8 (unit m/s²)