Question

Note: Enter your answer and show all the steps that you use to solve this problem in the spaceprovided

Answer 1

Given:

The point P(x,y) is given as,

`P(x,y)=P((33)/(65),y)`

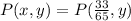
The objective is to find the value of sinθ.

Step-by-step explanation:

Since the terminal side of angleθ meets the unit circle, the general equation of circle can be represented as,

`\begin{gathered} x^2+y^2=1^2 \\ x^2+y^2=1\text{ . . . .. . (1)} \end{gathered}`

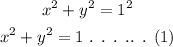
The position of point P on unit circle can be represented as,

To find y:

On further solving the equation (1),

`\begin{gathered} y^2=1-x^2 \\ y=\sqrt[]{1-x^2}\text{ . . . .. (2)} \end{gathered}`

On plugging the value of x in equation (2),

`y=\sqrt[]{1-((33)/(65))^2}`

On solving the equation for y,

`\begin{gathered} y=\sqrt[]{1-(1089)/(4225)} \\ =\sqrt[]{(4225-1089)/(4225)} \\ =\sqrt[]{(3136)/(4225)} \\ =\pm(56)/(65) \end{gathered}`

Thus, the value of sinθ will be,

`\sin \theta=\pm(56)/(65)`

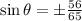
Since P is in IV quadrant,

`\sin \theta=-(56)/(65)`

Hence, the value of sinθ=-56/65.