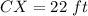we know that
The centroid is the point where all three medians intersect and divides each median in a ratio of
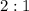 . Is described as the triangle's center of gravity.
. Is described as the triangle's center of gravity.
In this problem
C-H, B-G and A-F ------> are medians
The point X is the centroid of the triangle ABC
so
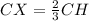
we have
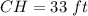
substitute
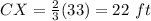
therefore
the answer is