Question

1.without using a calculator, find all the roots of the equation.

a. x^3+x^2+4x+4=0
b. x^3+4x^2+x-6=0
c. x^4-4x^3+x^2+12x-12=0

2.find all the zeros of the function
a. y=x^4-6x^2+8
b. y=x^3+6x^2+x+6
c. g(x)=x^3-4x^2-x+22
d. y=x^4-x^3-5x^2-x-6

Answer 1

b. x^3+4x^2+x-6=0

and

d. y=x^4-x^3-5x^2-x-6

Answer 2

Part 1A:

Given


`x^3+x^2+4x+4=0 \\ \\ \Rightarrow x^2(x+1)+4(x+1)=0 \\ \\ \Rightarrow(x^2+4)(x+1)=0 \\ \\ \Rightarrow x= -1\ or\ x=\pm2i`



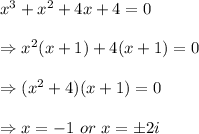
Part 1B:

Given


`x^3+4x^2+x-6=0`

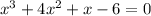
Using rational roots theorem, we can see that the possible roots of the the given equation are:
`\pm1,\ \pm2,\ \pm3,\ \pm6`

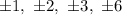
By substituting the possible roots, we can see that x = 1 is a root, thus x - 1 is a factor.
We can get the other factors by using sythetic division to divide
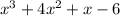
`x^3+4x^2+x-6` by x - 1.

1 | 1 4 1 -6
|
| 1 5 6
|_____________
1 5 6 0

Thus the other factor is
`x^2+5x+6=(x+2)(x+3)`

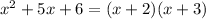
Therefore, all the roots of
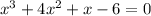
`x^3+4x^2+x-6=0` are x = 1, x = -2 and x = -3.



Part 1C:

Given


`x^4-4x^3+x^2+12x-12=0`

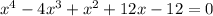
Using rational roots theorem, we can see that the possible roots of the the given equation are:
`\pm1,\ \pm2,\ \pm3,\ \pm4,\ \pm6,\ \pm12`

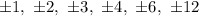
By substituting the possible roots, we can see that x = 2 is a root, thus x - 2 is a factor.
We can get the other factors by using sythetic division to divide
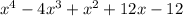
`x^4-4x^3+x^2+12x-12` by x - 2.

2 | 1 -4 1 12 -12
|
| 2 -4 -6 12
|____________________
1 -2 -3 6 0

Thus the other factor is
`2x^3-4x^2-6x+12`

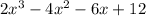
Thus, we have


`2x^3-4x^2-6x+12=0 \\ \\ \Rightarrow x^3-2x^2-3x+6=0 \\ \\ \Rightarrow x^2(x-2)-3(x-2)=0 \\ \\ \Rightarrow(x^2-3)(x-2)=0 \\ \\ \Rightarrow x=\pm√(3)\ or\ x=2`

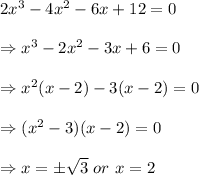
Therefore, all the roots of
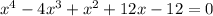
`x^4-4x^3+x^2+12x-12=0` are x = 2,
`x=\pm√(3)`.



Part 2A:

Given


`y=x^4-6x^2+8`

The zero of the function is when y = 0, thus we have


`x^4-6x^2+8=0 \\ \\ \Rightarrow x^4-2x^2-4x^2+8=0 \\ \\ \Rightarrow x^2(x^2-2)-4(x^2-2)=0 \\ \\ \Rightarrow(x^2-4)(x^2-2)=0 \\ \\ \Rightarrow x=\pm2\ or\ x=\pm√(2)`



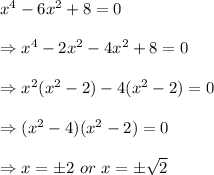
Part 2B:

Given


`y=x^3+6x^2+x+6`

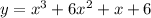
The zero of the funtion is when y = 0, thus we have


`x^3+6x^2+x+6=0 \\ \\ \Rightarrow x^2(x+6)+1(x+6)=0 \\ \\ \Rightarrow(x^2+1)(x+6)=0 \\ \\ \Rightarrow x=\pm i\ or\ x=-6`



Part 2C:

Given


`g(x)=x^3-4x^2-x+22`

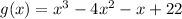
Using rational zeros theorem, we can see that the possible zeros of the the given equation are:
`\pm1,\ \pm2,\ \pm11,\ \pm22`

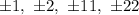
By substituting the possible zeros, we can see that x = -2 is a zero, thus x + 2 is a factor.
We can get the other factors by using sythetic division to divide
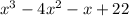
`x^3-4x^2-x+22` by x + 2.

-2 | 1 -4 -1 22
|
| -2 12 -22
|____________________
1 -6 11 0

Thus the other factor is


`-2x^2+12x-22=0\\ \\ \Rightarrow x^2-6x+11=0 \\ \\ \Rightarrow x= (-(-6)\pm√((-6)^2-4(11)))/(2) \\ \\ = (6\pm√(-8))/(2) =(6\pm2√(2)i)/(2)=3\pm i√(2)`

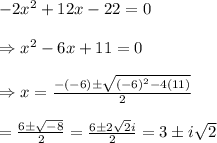
Therefore, all the zeros of
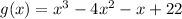
`g(x)=x^3-4x^2-x+22` are x = -2,
`x=3\pm i√(2)`.



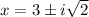
Part 2D:

Given


`y=x^4-x^3-5x^2-x-6`

Using rational zeros theorem, we can see that the possible zeros of the the given equation are:
`\pm1,\ \pm2,\ \pm3,\ \pm6`

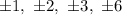
By substituting the possible zeros, we can see that x = -2 is a zero, thus x + 2 is a factor.
We can get the other factors by using sythetic division to divide
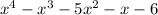
`x^4-x^3-5x^2-x-6` by x + 2.

-2 | 1 -1 -5 -1 -6
|
| -2 6 -2 6
|____________________
1 -3 1 -3 0

Thus the other factor is


`-2x^3+6x^2-2x+6=0 \\ \\ \Rightarrow x^3-3x^2+x-3=0 \\ \\ \Rightarrow x^2(x-3)+1(x-3)=0 \\ \\ \Rightarrow(x^2+1)(x-3)=0 \\ \\ \Rightarrow x=\pm i\ or\ x=3`

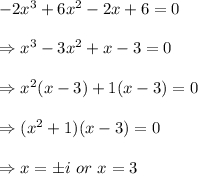
Therefore, all the zeros of
`y=x^4-x^3-5x^2-x-6` are x = -2, x = 3,
`x=\pm i`.