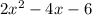Question

The area of a rectangles x2 - 2x - 3. If one of the adjacent sides has length (x + 1), determine the length of the other side and hence find an expression for the perimeter of the rectangle in simplest form.

Answer 1

Given:

The area of a rectangles

`x^2-2x-3`

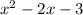
And one of the adjacent sides has length is,

`(x+1)`

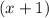
Required:

To find the other side, and find an expression for the perimeter of the rectangle in simplest form.

Step-by-step explanation:

`A=L* W`
`\begin{gathered} x^2-2x-3=(x+1)* W \\ \\ W=(x^2-2x-3)/(x+1) \end{gathered}`
`\begin{gathered} \text{ x-3} \\ x+1)x^2-2x-3 \\ \text{ x}^2+x \\ =-3x-3 \\ -3x-3 \\ =0 \end{gathered}`

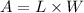
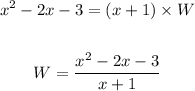
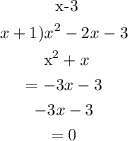
Therefore, the other side is

`(x-3)`

The perimeter of a rectangle is,

`\begin{gathered} P=2A \\ \\ =2(x^2-2x-3) \\ \\ =2x^2-4x-6 \end{gathered}`

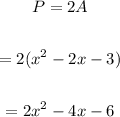
Final Answer:

The other side of the rectangle is,

`(x-3)`

The perimeter is,

`2x^2-4x-6`