Question

A rectangular swimming pool has a length of 11 feet, a width of 25 feet and a depth of 5 feet. Roundyour anwers to the nearest hundredth as needed.(a) How many cubic feet of water can the pool hold?(b) The manufacturer suggests filling the pool to 95% capacity. How many cubic feet of water is this?ft³(c) One cubic foot of water is approximately 7.48 gallons. How many gallons of water should you putin the pool at 95% capacity?gallons(d) A gallon of water weighs approxaimtely 8.35 pounds. How many pounds of water are in the poolat 95% capacity?pounds

Answer 1

- The formula for finding the volume of a rectangular prism is:

`\begin{gathered} V=l* w* h \\ where, \\ l=length \\ w=width \\ h=height \end{gathered}`

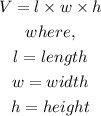
- Since the swimming pool is in the shape of a rectangular prism, we can proceed to solve as follows:

Question A:

- The amount of water the pool can hold is calculated below:

`V=11*25*5=1375ft^3`

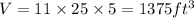
Question B:

- If 95% of the pool must be filled, then, we can say:

`\begin{gathered} (95)/(100)*1375 \\ \\ =1306.25ft^3 \end{gathered}`

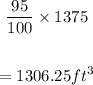
Question C:

`\begin{gathered} 1ft^3\to7.48gallons \\ \therefore1306.25ft^3\to x\text{ gallons} \\ \\ (1ft^3)/(1306.25ft^3)=\frac{7.48\text{ gallons}}{x\text{ gallons}} \\ \\ \therefore x=\frac{7.48\text{ gallons }*1306.25ft^3}{1ft^3} \\ \\ x=9770.75gallons \end{gathered}`

Question D:

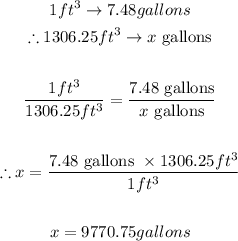
`\begin{gathered} 1\text{ gallon}\to8.35\text{ pounds} \\ \therefore9770.75\text{ gallons}\to x\text{ pounds} \\ \\ \frac{1\text{ gallon}}{9770.75\text{ gallons}}=\frac{8.35\text{ pounds}}{x\text{ pounds}} \\ \\ \therefore x=(9770.75*8.35)/(1)\text{ pounds} \\ \\ x=81585.7625\approx81585.76\text{ pounds \lparen To the nearest hundredth\rparen} \end{gathered}`

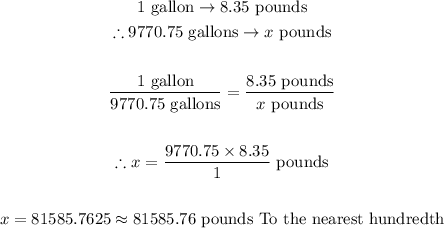
Final Answer

Question A:

1375 cubic feet

Question B:

1306.25 cubic feet

Question C:

9770.75 gallons

Question D:

81585.76 pounds