Question

Trapezoid WXYZ has vertices W(−1, 2) , X(2, 2) , Y(3, −1) , and Z(−3, −1) .

Is the trapezoid an isosceles trapezoid?



Select from the drop-down menu to correctly complete the statement.

Answer 1

she is right its ( is not) just took the test

Answer 2

The given trapezium is not an isosceles trapezium.

Explanation:

Given:

Coordinates of the vertices of a trapezium:

• 
  `W (x_w,y_w)=(-1,2)`

• 
  `X(x_x,y_x)=(2,2)`

• 
  `Y(x_y,y_y)=(3,-1)`

• 
  `Z(x_z,y_z)=(-3,-1)`

A trapezoid is a convex-quadrilateral whose one pair of opposite sides are parallel but not equal in length, which lead to a pair of non-parallel sides.

• It holds all the properties of a convex- quadrilateral.

• When the non-parallel sides of the the trapezium are equal in length then the trapezium is said to be isosceles.

From the attached schematic we find the length of the non-parallel sides.

We know that the distance between two points can be evaluated as:

`XY=√((x_x-x_y)^2+(y_x-y_y)^2)`

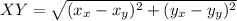
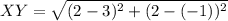
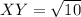`XY=√((2-3)^2+(2-(-1))^2)`

`XY=√(10)` ..............................................(1)

Now,

`ZW=√((x_z-x_w)^2+(y_z-y_w)^2)`

`ZW=√((-3-(-1))^2+(-1-2)^2)`

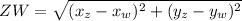
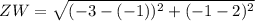
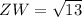`ZW=√(13)` .........................................(2)

Therefore, from eq. (1) & (2) we can conclude that the given trapezium is not an isosceles trapezium.