We are given a linear graph of position vs time and we are asked to determine the velocity at 40 seconds. To do that we need to take into account that the velocity in a graph of position vs time is given by the slope of the line. Therefore, we need to determine the slope of the line above the 40 seconds. To determine the slope we will use the following formula:

This means that we need to pick two points on the line above 40 seconds. To pick the points we use the graph, like this:
The points we have picked are:
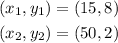
Replacing in the formula for the slope:

Solving the operations:
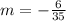
Rewriting as a fraction:
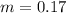
The velocity is 0.17 meters per second.
For part B, to determine the average velocity we will use the following formula:
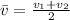
This means that we need to add the velocities for each of the slopes of the lines and divide the result by 2. Replacing we get:
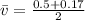
Solving the operations we get:
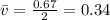
Therefore, the average velocity is 0.34 meters per second.