Question

There is a rectangular garden with an area of 24 square feet. The garden is 2 feetlonger than it is wide Create an equation that can be used to determine the length and wath of the garden.

Answer 1

We know that

• The area is 24 square feet.

,

• The length is 2 feet longer than its width.

The area of a rectangle is

`A=w* l`

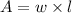
Where,

`\begin{gathered} A=24 \\ l=w+2 \end{gathered}`

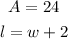
Let's replace these expressions

`24=w*(w+2)`

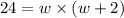
Now, we solve for w

`24=w^2+2w`

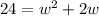
Let's solve this quadratic equation

`w^2+2w-24=0`

We have to look for two numbers whose product is 24 and whose difference is 2. Those numbers are 6 and 4.

`w^2+2w-24=(w+6)(w-4)`

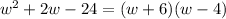
The solutions are w = -6, and w = 4. Where the positive solution makes sense to the problem only.

If the width is 4 feet, then the length is 6 feet (because it's 2 feet longer than the width).

Hence, the dimensions of the garden are 4 feet wide by 6 feet long.