Solution
- We need to find the expression for the population and the way to do that is to integrate both sides with respect to time.
- After this, we can then apply the values given to solve the question.
- This is done below:
![\begin{gathered} (dP)/(dt)=kP \\ \\ \text{ Rearrange} \\ (dP)/(P)=kdt \\ \\ \text{ Integrate both sides} \\ \int(dP)/(P)=\int kdt \\ \\ \ln P=kt+C \\ \text{ Take the }e\text{ exponent of both sides} \\ \\ e^(\ln P)=e^(kt+C) \\ \\ \text{ But we know that }e^(\ln x)=x \\ \\ \text{ Thus, we have that:} \\ P=e^(kt+C)=e^(kt).e^C \\ \text{ Let }A=e^C,\text{ since }e^C\text{ is a constant} \\ \\ \therefore P=Ae^(kt) \\ \\ \\ \\ Now\text{ that we have the expression for P, let us find the values of }A,\text{ and }k\text{ using the values} \\ given. \\ \\ \text{ when }P=40000,t=3: \\ 40000=Ae^(3k) \\ when\text{ }P=50000,t=5: \\ 50000=Ae^(5k) \\ \\ \text{ Divide both equations} \\ (50000)/(40000)=(Ae^(5k))/(Ae^(3k)) \\ \\ (5)/(4)=e^(5k-3k)=e^(2k) \\ \\ \text{ Take the natural log of both sides} \\ \ln(5)/(4)=\ln e^(2k)=2k \\ \\ \therefore k=(1)/(2)\ln((5)/(4))=\ln(√(5))/(2) \\ \\ \text{ Putting this value of }k\text{ into any of the two equations,} \\ 40000=Ae^{\ln(√(5))/(2)*3}=Ae^{\ln((√(5))/(2))^3} \\ 40000=A*((√(5))/(2))^3=A*(5√(5))/(8) \\ \\ A=(40000*8)/(5√(5))=(64,000)/(√(5))*(√(5))/(√(5))=12,800√(5) \\ \\ \\ \text{ Thus, our population equation is:} \\ P=12,800√(5)e^{\ln((√(5))/(2))^t} \\ P=12,800√(5)((√(5))/(2))^t \end{gathered}]()
- Now that we have the expression for P, we can thus evaluate it at t = 10 as follows:
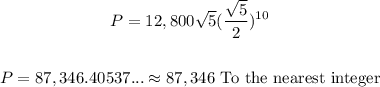
Final Answer
The population is 87,346