Question

Mr Smith's art class took a bus trip to an art museum. The bus averaged 65 miles per hour on the highway and 25 miles per hour in the city. The art museum is 375 hours away for the school and it took the class 7 hours to get there. Use Cramer's rule to find out how many hours the bus was on the highway and how many hours it was driving in the city.

Answer 1

Let x be the distance traveled on the highway and y the distance traveled in the city, so:

`\left \{ {{x+y=375} \atop { (1)/(65)x+ (1)/(25)y =7}} \right.`

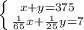
Now, the system of equations in matrix form will be:

`\left[\begin{array}{ccc}1&1&\\ (1)/(65) & (1)/(25) &\end{array}\right] \left[\begin{array}{ccc}x&\\y&\end{array}\right] = \left[\begin{array}{ccc}375&\\7&\end{array}\right]`

Next, we are going to find the determinant:

`D= \left[\begin{array}{ccc}1&1\\ (1)/(65) & (1)/(25) \end{array}\right] =(1)( (1)/(25)) - (1)( (1)/(65) )= (8)/(325)`
Next, we are going to find the determinant of x:

`D_(x) = \left[\begin{array}{ccc}375&1\\7& (1)/(25) \end{array}\right] = (375)( (1)/(25) )-(1)(7)=8`

Now, we can find x:

`x= ( D_(x) )/(D) = (8)/( (8)/(325) ) =325mi`

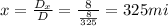
Now that we know the value of x, we can find y:

`y=375-325=50mi`

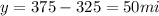
Remember that time equals distance over velocity; therefore, the time on the highway will be:

`t_(h) = (325)/(65) =5hours`
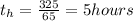
An the time on the city will be:

`t_(c) = (50)/(25) =2hours`

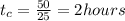
We can conclude that the bus was five hours on the highway and two hours in the city.