Question

Mrs. Lindsay doesn't have a cat crate and needs to take her cats to the vet. She'sgoing to make a box out of a 4 foot by 4 foot piece of cardboard. What dimensionsshould Mrs. Lindsay cut from the corners of the box in order to have the maximumamount of space inside to fit her cats. What is the volume inside the box to give Mrs.Lindsay the maximum amount of space inside the box?6.5 ft3.2 ft5.8 ft4.7ft²

Answer 1

Answer is 4.7

If Mrs. Lindsay cuts out portions of the edges of the cardboard of 4ft by 4ft,

she can do it in the manner depicted below:

If the portion cut out at the edges of the cardboard are r by r in area.

This means that when she wants to form the cat box, the edges she has to work with are:

(4-2r), (4-2r) and r as length (l), width (w) and height (h) respectively.

The formula for Volume of a box is:

V = l x w x h

Thus, we have:

`\begin{gathered} V=(4-2r)*(4-2r)* r \\ \text{Expanding the bracket} \\ V=16r-16r^2+4r^3 \\ \end{gathered}`

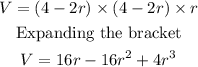
This gives the equation for getting the volume of the box in terms of the edges she cuts off.

Now, the question asks us for the maximum volume she can form. Therefore, we need to find the equation of the rate of change of Volume (V). We can then equate this expression for V to zero because at the maximum Volume, the Volume cannot change anymore unless it is reducing.

Thus, we can solve:

`\begin{gathered} (dV)/(dr)=16-32r+12r^2 \\ \\ (dV)/(dr)=0\text{ (At maximum Volume)} \\ \\ 12r^2-32r+16=0 \end{gathered}`

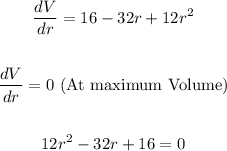
We need to solve this quadratic equation:

`\begin{gathered} 12r^2-24r-8r+16=0_{} \\ \text{factorize,} \\ 12r(r-2)-8(r-2)=0 \\ (12r-8)(r-2)=\text{ 0} \\ \therefore r=2\text{ or r=}(8)/(12)=(2)/(3) \end{gathered}`

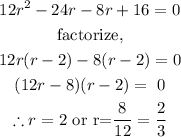
Now that we have the possible values of r when V is maximum, we can proceed to test whether or not these points r = 2 or r = 2/3 are maximum values.

The way to know is that the second derivative of the equation of volume (V) must be less than 0

i.e.

`(d^2V)/(dr^2)<0`

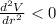
Therefore, we can solve:

`\begin{gathered} (d^2V)/(dr^2)=-32+24r \\ \text{when r=2} \\ (d^2V)/(dr^2)=-32+24(2)=16 \\ 16\\leqslant0 \\ \\ \text{when r=}(2)/(3) \\ (d^2V)/(dr^2)=-32+24((2)/(3))=-16\text{ < 0} \end{gathered}`

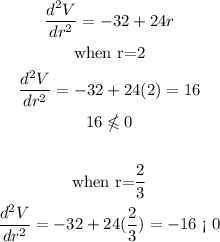
Therefore, the value of r that gives the maximum volume is:

`r=(2)/(3)`

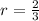
Therefore, to calculate the Maximum volume, we only need to plug in this value of r into the equation of V

`\begin{gathered} V=4r^3-16r^2+16r \\ \text{put r=}(2)/(3) \\ \\ V=4((2)/(3))^3-16((2)/(3))^2+16((2)/(3)) \\ V=1.1852-7.1111+10.6667 \\ V=4.7408ft^3 \end{gathered}`

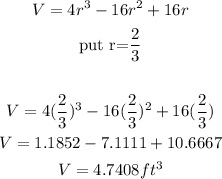
Thus answer is:

V = 4.7