Question

Solve 3|x+1| -2 < 4.A) -3 < xor x < 1B) -3 1C) -3 < x < 1OD) -3 < x and x > 1

Answer 1

C) -3 < x < 1

Explanation:

Given the absolute inequality:

`3|x+1|-2<4`

First, add 2 to both sides of the equation:

`\begin{gathered} 3|x+1|-2+2<4+2 \\ 3\lvert x+1\rvert\lt6 \end{gathered}`

Next, divide both sides by 3:

`\begin{gathered} (3|x+1|)/(3)<(6)/(3) \\ |x+1|<2 \end{gathered}`

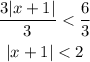
We then solve the absolute inequality:

[tex]\begin{gathered} -2The solution to the absolute inequality is -3Option C is correct.