Question

Determine whether the given lengths can be sides of a right triangle.

Which of the following are true statements?
A. The lengths 14, 24 and 26 can be sides of a right triangle. The lengths 30, 72, and 78 can be sides of a right triangle.
B.The lengths 14, 24 and 26 cannot be sides of a right triangle. The lengths 30, 72, and 78 can be sides of a right triangle.
C.The lengths 14, 24 and 26 cannot be sides of a right triangle. The lengths 30, 72, and 78 cannot be sides of a right triangle.
D.The lengths 14, 24 and 26 can be sides of a right triangle. The lengths 30, 72, and 78 cannot be sides of a right triangle.

Answer 1

The lengths 14, 24 and 26 can be sides of a right triangle. The lengths 30, 72, and 78 can not be sides of a right triangle.

Answer 2

Answer: The correct option is (B). The lengths 14, 24 and 26 cannot be sides of a right triangle. The lengths 30, 72, and 78 can be sides of a right triangle.

Step-by-step explanation: We are given to determine whether the given lengths can be sides of a right triangle.

The lengths of the sides of two triangles are (14, 24, 26) and (30, 72, 78).

For a right-angled triangle, the square of the length of the largest side (Hypotenuse) is equal to the sum of the squares of the lengths of the other two sides (Perpendicular and Base).

That is,

Hypotenuse² = Perpendicular² + Base² .

For the side lengths 14, 24 and 26, we have

`26^2=676,\\\\14^2+24^2=196+576=772.`

So, Hypotenuse² ≠ Perpendicular² + Base² .

Therefore, this triangle is not a RIGHT-angled triangle.

For the side lengths 30, 72 and 78, we have

`78^2=6084,\\\\30^2+72^2=900+5184=6084.`

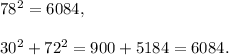
So, Hypotenuse² = Perpendicular² + Base² .

Therefore, this triangle is a RIGHT-angled triangle.

So, the triangle with side lengths 14, 24 and 26 cannot be a Right-angled triangle and the triangle with side lengths 30, 72 and 78 can be a Right-angled triangle.

Thus, option (B) is the correct option.