Question

Hello,How can I find the difference quotient of the following?

Answer 1

The difference quotient is used to calculate the average rate of change of a function over a given interval.

Step-by-step explanation:

The difference quotient is used to calculate the average rate of change of a function over a given interval. To find the difference quotient, you need to evaluate the function at two different points and then divide the difference in function values by the difference in the x-values of those points. Mathematically, the difference quotient is expressed as:

(f(x+h) - f(x))/h

where 'f(x)' represents the function and 'h' represents the difference in x-values.

Answer 2

The given function as;

f(x) = x² - 8x + 3

f(x + h) , susbtitute x = x + h in the given expression as;

f(x+h) = (x+h)² - 8(x+h) + 3

f(x+h) = (x² + h² + 2xh) -8x - 8h + 3

f(x+h) = x² + h² + 2xh - 8x - 8h + 3

Now substitute the value of f(x+h) in the expression as;

`\begin{gathered} (f(x+h)-f(x))/(h)=((x^2+h^2+2xh-8x-8h+3)-(x^2-8x+3))/(h) \\ (f(x+h)-f(x))/(h)=(x^2+h^2+2xh-8x-8h+3-x^2+8x-3)/(h) \\ (f(x+h)-f(x))/(h)=(x^2-x^2+h^2+2xh-8x+8x-8h+3-3)/(h) \\ (f(x+h)-f(x))/(h)=(2xh+h^2-8h)/(h) \\ (f(x+h)-f(x))/(h)=(h(2x+h-8))/(h) \\ (f(x+h)-f(x))/(h)=2x+h-8 \end{gathered}`

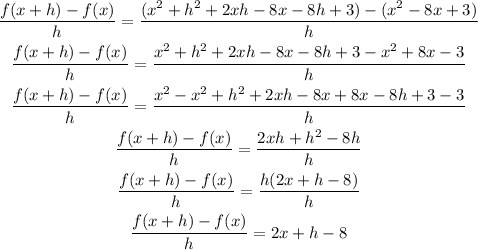
Answer : 2x + h - 8

.........