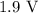Question

A parallel-plate capacitor consists of two identical, parallel, conducting plates each with an area of 5.0 cm2 and uniform charges of +8.4 pC or -8.4 pC. The plates are separated by a perpendicular distance of 1.0 mm. What is the potential difference across the metallic plates?

Answer 1

Given:

Area = 5.0 cm²

Uniform charges = +8.4 pC or -8.4 pC

Perendicular distance = 1.0 mm

Let's find the potential difference across the metallic plates.

To find the potential difference, apply the formula:

`V=(Q)/(C)`

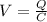
Where:

V is the potential difference

Q is the charge = 8.4 pC

C is the capacitance.

To find C, apply the formula:

`\begin{gathered} C=(E_oA)/(D) \\ \end{gathered}`

Where:

Eo = 8.85 x 10⁻¹² f/m

A is the area

D is the distance.

Thus, we have:

`\begin{gathered} C=((8.85*10^(-12))(5.0*10^(-4)))/(1.0*10^(-3)) \\ \\ C=4.425*10^(-12)\text{ F} \end{gathered}`

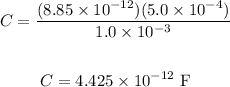
Now, to find the potential difference, we have:

`\begin{gathered} V=(Q)/(C) \\ \\ V=(8.4*10^(-12))/(4.425*10^(-12)) \\ \\ V=1.89\text{ V }\approx1.9\text{ V} \end{gathered}`

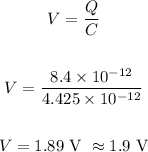
The potential difference across the metallic plates is 1.9 volts

ANSWER:

`1.9\text{ V}`