Question

Which statement best reflects the solution(s) of the equation? √2x−1−x+2=0

answer choices:

There is only one solution: x = 1. The solution x = 5 is an extraneous solution.

There are two solutions: x = 1 and x = 5.

 There is only one solution: x = 5. The solution x = 1 is an extraneous solution.

There is only one solution: x = 5. The solution x = 0 is an extraneous solution.

Answer 1

Simplifing the expression and moving to the RHS we have âš2x = x +1 Let's check for extraneous solution by squaring both sides. I assume the x and 2 are together. So we have 2x = (x+1)^2 This gives 2x = x^2 + 2x +1. So x^2 + 2x +1 -2x = 0. Then we have x^2 =-1. When x =1; 1 is not equal to -1 so x =1 is an extraneous solution.

Answer 2

There is only one solution: x = 5. The solution x = 1 is an extraneous solution.

Explanation:

The given expression is

`√(2x-1) -x+2=0`

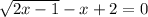
We rewrite the expression so that we equate everything to zero to obtain,

`√(2x-1) =x-2`

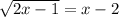
We now square both sides to obtain,

`(√(2x-1))^2 =(x-2)^2`

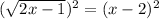
This simplifies to give us,

`2x-1=(x-2)^2`

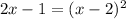
We now expand the parenthesis to get,

`2x-1=x^2-4x+4`

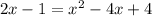
We now group the terms so that we can obtain the quadratic equation;

`0=x^2-4x-2x+4+1`

`0=x^2-6x+5`

`x^2-6x+5=0`

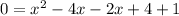
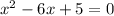
We split the middle term to obtain,

`x^2-x-5x+5=0`

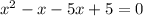
We factor to obtain,

`x(x-1)-5(x-1)=0`

`(x-1)(x-5)=0`

`\Rightarrow (x-1)=0\:or\:(x-5)=0`

`\Rightarrow x=1\:or\:x=5`

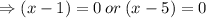
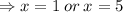
Let us check to see whether the two values satisfy the given equation.

When
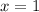`x=1`, we get,

`√(2(1)-1) -1+2=0`

`\Rightarrow √(1) +1=0`

`\Rightarrow 1 +1=0`

`\Rightarrow 2=0`

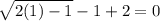
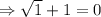
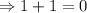
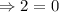
This statement is false. Hence
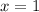`x=1` is an extraneous solution.

When
`x=5`, we get,

`√(2(5)-1) -5+2=0`

`\Rightarrow √(9) -3=0`

`\Rightarrow 3-3=0`

`\Rightarrow 0=0`

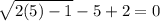
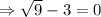
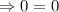
This statement is very trues.

Therefore
`x=5` is the only solution.

There is only one solution: x = 5. The solution x = 1 is an extraneous solution.