Question

One factor of the function f(x)=3^3-9x^2+20x-12 is (x-6). Describe how to find the x-intercept and the y-intercept of the graph of f(x) without using technology. Show your work and include all intercepts in your answer.

Answer 1

Given:

`f(x)=x^3-9x^2+20x-12`

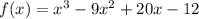
For y intercept the value of x=0

then :

`\begin{gathered} f(x)=y \\ f(x)=x^3-9x^2+20x-12 \\ y=(0)^3-9(0)^2+20(0)-12 \\ y=-12 \\ y=-12 \end{gathered}`

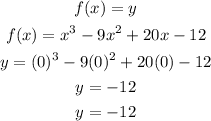
so y -intercept is -12.

For x intercept the value of y is zero.

`\begin{gathered} y=x^3-9x^2+20x-12 \\ y=0 \\ x^3-9x^2+20x-12=0 \end{gathered}`

If one factor is (x-6) then other factor is:

`=(x^3-9x^2+20x-12)/(x-6)`

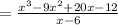
So all factor is:

`\begin{gathered} (x-6)(x^2-3x+2)=0 \\ x=6 \\ x^2-3x+2=0 \end{gathered}`

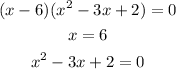
one x intercept 6 and another intercept is:

`\begin{gathered} x^2-3x+2=0 \\ x^2-2x-x+2=0 \\ x(x-2)-1(x-2)=0 \\ (x-2)(x-1)=0 \\ x=2 \\ x=1 \end{gathered}`

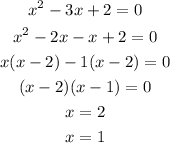
So x - intercept of graph is

1,2,6