If a point is in the graph of the parabola it needs to satisfy the equation. So we just need to find which values does not satisfy the equation
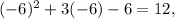
then the number A. IS on the graph
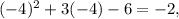
then the number B. IS on the graph
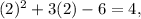
then the number B. IS on the graph, and finally
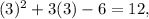
since this is diferent from -6, then (3,-6) is NOT on the graph. Then the answer is D. (3,-6)
The point-slope form is
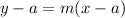
we find the slope using the formula

Replacing this, and the point (-2,3)
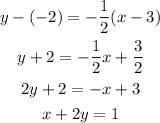
The equation of the line is x+2y=1