Question

Find an equation of the line parallel to the graph of y = 3/2x + 3 that passesthrough the point of (4,4). Write your equation in slope-intercept form.

Answer 1

Consider that the equation of a straight line with slope (m) and y-intercept (c) is given by,

`y=mx+c`

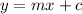
The given equation of the line is,

`y=(3)/(2)x+3`

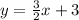
Comparing the coefficients, the slope of the given line is,

`m=(3)/(2)`

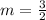
Let 'l' be the line parallel to the given line. Since both the lines are parallel, their slopes must also be equal. This implies that the slope of line 'l' is also 3/2 .

Then the equation of line 'l' is given by,

`\begin{gathered} y=mx+c \\ y=(3)/(2)x+c \end{gathered}`

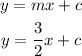
Given that line 'l' passes through the point (4,4), so it must satisfy the equation of its line,