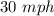we know that
The speed is equal to the distance divided by the time
Let
x---------> the distance Jessica's home to the grocery store
t1-------> the time from Jessica's home to the grocery store
t2------> the time from grocery store to back home
Step 1
Find the distance x
we have
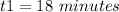
convert to hour
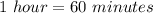
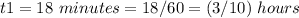

Step 2
Find the time t2
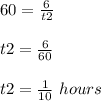
Step 3
Find the average speed for the entire trip
we know that
the average speed is equal
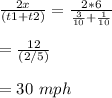
therefore
the answer is
the average speed for the entire trip is