Question

Mr. Smith traveled to a city 190 miles from his home to attend a meeting. Due tocar trouble, his average speed returning was 12 mph less than his speed going. Ifthe total time for the round trip was 7 hours, at what rate of speed did he travel tothe city? (Round your answer to the nearest tenth.)

Answer 1

Total distance (d)=190 miles.

Let, r be the rate of speed. and the going speed of the car is r mps.

and time is,

`\begin{gathered} \text{time}=\frac{dis\tan ce}{\text{speed}} \\ t=(190)/(r) \end{gathered}`

For returning ,

`\begin{gathered} \text{speed =r-12} \\ \text{time}=(190)/(r-12) \end{gathered}`

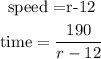
Total time is 7 hours.

So, it can be written as,

`\begin{gathered} (190)/(r)+(190)/(r-12)=7 \\ ((r-12)190+190r)/(r(r-12))=7 \\ 190r-2280+190r=7r^2-84r \\ 7r^2-464r+2280=0 \\ \text{compare with ax}^2+bx+c=0 \\ a=7,b=-464,\text{ c=2280} \\ r=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ r=(-\left(-464\right)\pm√(\left(-464\right)^2-4\cdot\:7\cdot\:2280))/(2\cdot\:7) \\ r=(-\left(-464\right)\pm\:4√(9466))/(2\cdot\:7) \\ r=(2\left(116+√(9466)\right))/(7),\: r=(2\left(116-√(9466)\right))/(7) \\ r=60.94\text{ , r=}5.34 \end{gathered}`

Now, check both the values of r ,For r=60.94

`\begin{gathered} (190)/(r)+(190)/(r-12)=(190)/(60.94)+(190)/(60.94-12) \\ =7 \end{gathered}`

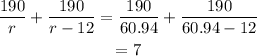
So, the speed of car is 60.94 mps.