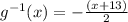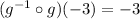Question

The one-to-one functions g and h are defined as follows.g(x) = -2x-13h=(-7 -2) (8)12I

Answer 1

We have to remember that in one-to-one functions each element of the domain maps to a different element in the range.

When we have a bijection we have that each element in the set A, for example, corresponds to exactly one element of B, and vice versa.

When we have a bijection, we also have an inverse function.

Then, we have that:

`g(x)=-2x-13`

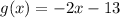
To find the inverse, we have to interchange the variables:

`y=-2x-13`

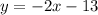
Now, we have:

`x=-2y-13`

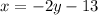
And we need to solve for y:

1. Add 13 to both sides of the equation:

`x+13=-2y-13+13\Rightarrow x+13=-2y`

2. Divide both sides by -2:

`((x+13))/(-2)=(-2y)/(-2)\Rightarrow-((x+13))/(2)=y`

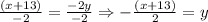
Then, we have that:

`g^(-1)(x)=-((x+13))/(2)`

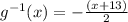
We can check this if we make a composition between the two functions (then we will get x as a result).

`(g^(-1)\circ g)=g^(-1)(g(x))=-\frac{((-2x-13)+13)_{}}{2}=-((-2x))/(2)=(2x)/(2)=x`

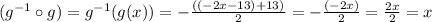
Then, we have that the result for this composition is equal to x. Thus:

`(g^(-1)\circ g)(-3)=-3^{}`

We also have that:

We have that h(4) = 3, then h^(-1)(3) = 4 or

`h(4)=3\Rightarrow h^(-1)(3)=4`

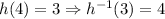
In summary, we have:

`g^(-1)(x)=-((x+13))/(2)`
`(g^(-1)\circ g)(-3)=-3`
`h^(-1)(3)=4`