Question

You randomly select two marbles from jar that contains 45black marbles, 15 white marbles and 10 red marbles. What isthe probability that the first marble is white and the secondmarble is not red if you do not replace the first marble? Enteryour answer as a decimal rounded to the nearest hundredth.-

Answer 1

We must keep in mind that from the Laplacian point of view, the probability of an event is the number of favorable cases over the number of possible cases. In addition, we will use combinatorics to count these cases. If we call

A: The first marble is white

B: the second marble is not red

We want to find P(A n B) and we assume that the events are independent since there is no replacement. So,

`P(A\text{ }\cap\text{ }B)=(15)/(45+15+10)\cdot(45+15-1)/(45+15+10-1)=(15)/(70)\cdot(59)/(69)=(59)/(322)\approx0.183`

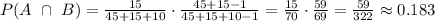
Thus, the answer is that the probability that the first marble is white and the second marble is not red if you do not replace the first marble is 0.183