Here we have to use the empirical rules of a gaussian distribution to find out this probability. We want to know the probability that one of the new parts produced will be over 1.412 cm, and this value is the mean plus 2 times the standard deviation.
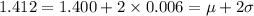
We know from the empirical rules, that 95% of the data falls within two standard deviations of the mean, then the amount of data out of this range is only 5%. Since the the normal distribution is symetric and we only want the positive side(over two times the standard deviation), our result is this probability divided by 2.
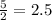
Then, this is our answer. The probability that one of the new parts produced will be over 1.412 cm long is 2.5%.