Question

Find the value of EF in the triangle below.H8FE4O 472O 43O8V2

Answer 1

From the triangle shown, we have three important informations:

- It is a right triangle, because it has a right angle, mHEF.

- Its hypotenuse has length 8, HF = 8.

- Its two legs has the same length, HE = EF.

Because it is a right triangle, we can use the Pythagora's Theorem:

`HE^2+EF^2=HF^2`

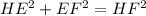
And we know that:

`\begin{gathered} HE=EF \\ HF=8 \end{gathered}`

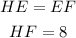
Thus:

`\begin{gathered} EF^2+EF^2=8^2 \\ 2EF^2=64 \\ EF^2=32 \\ EF=\sqrt[]{32} \\ EF=\sqrt[]{2^5} \\ EF=4\sqrt[]{2} \end{gathered}`