ANSWER
(-6, -7)
Step-by-step explanation
We have that the midpoint of A and B is M (-1, -5).
The midpoint, M, of two points A(x1, y1) and B(x2, y2) is given as:
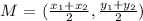
We are given that:
(x1, y1) = (4, -3)
We need to find (x2, y2).
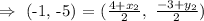
Now, compare the x and y cordinates separately.
For x:
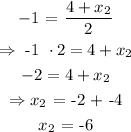
For y:
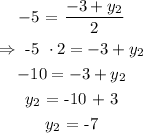
So, the cordinates of B are (-6, -7)