Question

How many solutions does this nonlinear system of equations have?5.5-5-5.OA. TwoB. OneC. FourD. Zero

Answer 1

Hello there. To solve this question, there are two ways.

We can determine the equations for both functions and solve the system or solve it by inspection, with mathematical arguments.

First, the red graph is a parabola, which is a quadratic function.

Hence why it is called a nonlinear system of equations, since one of the equations has degree two.

Notice it passes through (0, 0), (-2, 2) and (2, 2), such that we can determine its equation. It has the form

`ax^2+bx+c`

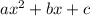
Such that we plug the values

`\begin{gathered} a\cdot0^2+b\cdot0+c=0\Rightarrow c=0 \\ \\ a\cdot2^2+b\cdot2=2\Rightarrow4a+2b=2 \\ \\ a\cdot(-2)^2+b\cdot(-2)=4a-2b=2 \\ \end{gathered}`

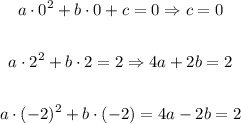
Adding the second and third equations, we get

`\begin{gathered} 8a=4\Rightarrow a=(4)/(8)=(1)/(2) \\ \end{gathered}`

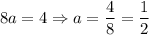
Such that the other constant is

`\begin{gathered} 4\cdot(1)/(2)+2b=2 \\ \\ 2+2b=2 \\ \\ 2b=0\Rightarrow b=0 \end{gathered}`

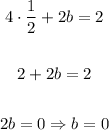
Therefore the equation is

`(1)/(2)x^2`

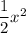
We cannot determine the equation of the line since any of the points of the images are contained in it.

This means we have to use the second approach:

The line is tangent to the parabola, which means they touches on a single point, called the point of tangency.

Hence the answer is:

The number of solutions of this nonlinear system of equations is one.