Solution
Step 1
Write out the expression of compound probability that will enable us solve the problem
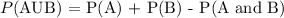
Where,
P(AUB) = students that play both string and brass instruments =?
P(A) = Students that play only brass instruments = 10 +5 students that play both= 15
P(B) = Students that play only string instruments=35 + 5 stdents that play both = 40
P(A and B) = Students that do not play either brass and string instruments =5
Step 2
Find the probability that a randomly selected student plays either the string or brass instrument (P(AUB)) by substitution
P(AUB) = 15 + 40 -5 = 50 students
Step 3
Write an expression for the probability of an event occurring
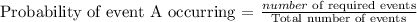
Number of events = 50
Total number of events = 35 + 10 +5+5 = 55
Step 4
Get the required answer after substitution
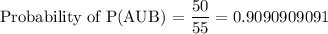
Hence the probability that a randomly selected student plays either a string or brass instrument is 0.9090909091