Question

Which translation maps the vertex of the graph of the function f(x) = x2 onto the vertex of the function g(x) = x2 + 2x +1?

right 1 unit
left 1 unit
right 2 units
left 2 units

Answer 1

Shift 1 unit left

B is correct

Step-by-step explanation:

Given: The vertex of f(x) shift to g(x)

`f(x)=x^2`

Vertex of f(x): (0,0)

`g(x)=x^2+2x+1`

Vertex form:
`y=a(x-h)^2+k`

`g(x)=(x+1)^2`

Vertex of g(x): (-1,0)

`(0,0)\rightarrow (-1,0)`

Only x-coordinate change and y-coordinate remain same.

`0\rightarrow -1`

Hence, The vertex of f(x) shift 1 unit left to get vertex of g(x)

Answer 2

Option B is correct

Left 1 unit.

Step-by-step explanation:

According to the graph theory of transformation:

y = f(x+k)=
`\left \{ {{k>0 shift graph of y= f(x) left k unit} \atop {k<0} shift graph of y= f(x) right |k| unit} \right.`

Given the parent function:
`f(x)=x^2`

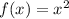
and the function
`g(x)=x^2+2x+1`

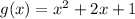
we can write it as:

g(x)=
`(x+1)^2` [ ∴
`(a+b)^2 = a^2+2ab+b^2` ]

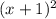Therefore, vertex of the graph of the function
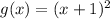`g(x)=(x+1)^2` is 1 units to the left of the vertex of the graph of the function
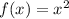`f(x)=x^2` .