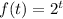Answer:
Given that,
Some of the functions of t given as,
f(t)=2^t
f(t)=0.5^t
f(t)=2t
f(t)=t^2+t+1
To find: The function grows the fastest for large values of t
Step-by-step explanation:
we get that given function are quadratic, linear and exponential.
Based on the definition,
The exponential function (b^t) with base (b) greater than 1 grows fastest for large values of t.
f(t)=2^t and f(t)=0.5^t are the two exponential functions, comparing the base, we get that,
2>1 and 2>0.5, we get that, The function grows the fastest for large values of t among the given function is,
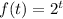
Answer is:
The function grows the fastest for large values of t is,