Question

The spread of a fungal infection in an ant colony

Answer 1

Given the equation:

`(dy)/(dt)=\frac{y+1}{2\sqrt[\placeholder{⬚}]{t}}`

When t=1, y=3 (three percent of the ants are infected).

Replacing in the equation:

`(dy)/(dt)=(3+1)/(2√(1))=2`

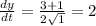
a) The equation of the line tangent to the graph is:

`\begin{gathered} y=3+2(t-1) \\ y=3+2t-2=2t+1 \end{gathered}`

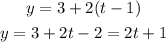
In t= 1.2.

`\begin{gathered} y(t)=2t+1 \\ y(1.2)=2(1.2)+1=3.4 \end{gathered}`

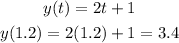
The percentage of the colony infected in t=1.2 is 3.4.

b) y explicity:

`\begin{gathered} (dy)/(dt)=(y+1)/(2√(t)) \\ \\ (dy)/(y+1)=\frac{dt}{2\sqrt[\placeholder{⬚}]{t}} \end{gathered}`

integrating both sides:

`\int(dy)/(y+1)=\int\frac{dt}{2\sqrt[\placeholder{⬚}]{t}}`

The first one will be:

`\begin{gathered} \int(dy)/(y+1) \\ u=y+1 \\ du=dy \\ \int(du)/(u)=ln(u)=ln(y+1)+c \end{gathered}`

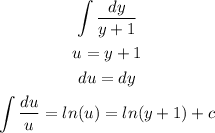
The second one, will be:

`\begin{gathered} (1)/(2)\int\frac{dt}{\sqrt[\placeholder{⬚}]{t}} \\ (1)/(2)\int t^{-(1)/(2)}dt=(1)/(2)*(\frac{t^{-(1)/(2)+1}}{-(1)/(2)+1})=(1)/(2)(\frac{t^{(1)/(2)}}{(1)/(2)})=t^{(1)/(2)}+k \\ \end{gathered}`

Substituing:

`ln(y+1)+c=t^{(1)/(2)}+k`

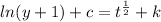
Using D=k-c

`\begin{gathered} ln(y+1)=t^{(1)/(2)}+D \\ y+1=e^{\sqrt[\placeholder{⬚}]{t}}*e^D \end{gathered}`

Finally:

`y=e^{\sqrt[\placeholder{⬚}]{t}}e^D-1`