Question

An aircraft travels with the wind for 120 miles in 0.75 of an hour. The return trip is flown against the wind and takes exactly 1 hour. Which system of linear equations represents x, the speed of the plane in miles per hour, and y, the speed of the wind in miles per hour? Recall the formula d = rt. 0.75(x + y) = 120 x − y = 120 0.75(x − y)= 120 x + y = 120 120(x + y) = 0.75 120(x − y) = 1 120(x − y) = 0.75 120(x + y) = 1 Mark this and return

Answer 1

n aircraft travels with the wind for 120 miles in 0.75 of an hour. The return trip is flown against the wind and takes exactly 1 hour.
Which system of linear equations represents x, the speed of the plane in miles per hour, and y, the speed of the wind in miles per hour?
---
With wind DATA:
distance = 120 miles ; time = (3/4)hr ; rate = 120/(3/4) = 160 mph
----
Against wind DATA:
distance = 120 miles ; time = 1 hr ; rate = 120 mph
-----

Equation::
Let p be speed of the plane in still air
Let w be speed of the wind
==================================
With wind:: p + w = 160 mph
Against wind:: p - w = 120 mph
================================

Answer 2

System of equation: 0.75(x+y)=120 and x-y=120

A is correct

Explanation:

An aircraft travels with the wind for 120 miles in 0.75 of an hour.

The return trip is flown against the wind and takes exactly 1 hour.

Let speed of aircraft be x mph and speed of wind y mph

Formula:

`speed=(Distance)/(Time)`

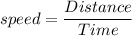
Case 1: When aircraft along with wind

Speed = x+y

Time = 0.75

Distance = 120

`x+y=(120)/(0.75)`

`0.75(x+y)=120`

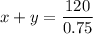
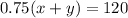
0.75(x+y)=120

Case 2: When aircraft against with wind

Speed = x-y

Time = 1

Distance = 120

`x-y=(120)/(1)=120`

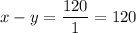
x-y=120

Hence, The system of equation are 0.75(x+y)=120 and x-y=120