Question

The hypotenuse of a right triangle is 24 ft. long. the length of one leg is 44 ft. more than the other. find the lengths of the legs.

Answer 1

The way to solve the missing side of a right triangle is normally by the Pythagorean Theorem:

`{a}^(2) + {b}^(2) = {c}^(2) \\ {a}^(2) = {c}^(2) - {b}^(2) \: \infty \: \sqrt{ {a}^(2) } = \sqrt{( {c}^(2) - {b}^(2)) } \\ a= \sqrt{( {c}^(2) - {b}^(2)) }`
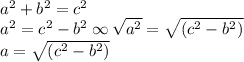
where c always is the hypotenuse
So c = 24 ft
b = 44 + a

`{a}^(2) + {b}^(2) = {c}^(2) \\ {a}^(2) + {(a + 44)}^(2) = {24}^(2) \\ {a}^(2) + {a}^(2) + 88a + 1936 = 576`
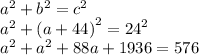
Now combine like terms:

`2{a}^(2) + 88a + 1936 = 576 \\ 2{a}^(2) + 88a + 1936 - 576 = 0 \\ 2{a}^(2) + 88a + 1360 = 0`
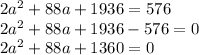
Now we have to try to factor this quadratic equation, first let's take out 2:

`2({a}^(2) + 44a + 680) = 0`
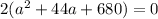
we need factors of 680 whose sum = 44
20×34, 10×68, 17×40
however... 20+34=54, 10+68=78, 17+40=57
So we will need to use the quadratic equation unfortunately :(

`x = ( - b + - \sqrt{( {b}^(2) - 4ac)}) / 2a`
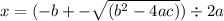
Now the "x" is actually our "a", the a is 1, b is 44, c is 680

`a = ( - 44 + - \sqrt{( {44}^(2) - 4(1)680)}) \\ / \: 2(1) \\ a = ( - b + - √((1936 - 2720))) \\ / \: 2`

`a = ( - 44 + - √((-784))) \\ / \: 2 = - 44 / 2 \: + - (i √(784)) / 2 \\ a = - 22 + - i √(16) √(49) / 2 \\`

`a = - 22 + - 28i / 2 \\ a = - 22 + - 14i`
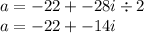
not quite sure where to go from these imaginary numbers...
I DON'T THINK A RIGHT TRIANGLE WITH THOSE DIMENSIONS IS POSSIBLE