we know that
The function cost is equal to

This is a vertical parabola open upward
The vertex is a minimum
The x-coordinate of the vertex represents the Number of airplane engines, that minimize the unit cost
The y-coordinate of the vertex is the minimum cost
Convert the given equation into vertex form
step 1
Factor 0.4
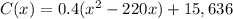
Complete the square

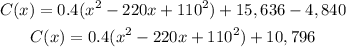
Rewrite as a perfect square

The vertex is the point (110,10,796)
therefore
The answer is 110 airplane engines