Question

What is the most precise name for quadrilateral ABCD with vertices A(−1,0), B(1,2), C(4,2), and D(2,0)?A. rhombusB. parallelogramC. squareD. rectangle

Answer 1

Let the 4 sides of the quadrilateral are AB, BC, CD, and DA.

Find the lengths of each side using the distance formulas as follows:

`\begin{gathered} AB=\sqrt[]{(1-(-1))^2+(2-0)^2} \\ =\sqrt[]{2^2+2^2} \\ =\sqrt[]{8} \end{gathered}`
`\begin{gathered} BC=\sqrt[]{(4-1)^2+(2-2)^2} \\ =\sqrt[]{3^2+0^2} \\ =3 \end{gathered}`
`\begin{gathered} CD=\sqrt[]{(2-4)^2+(0-2)^2} \\ =\sqrt[]{(-2)^2+(-2)^2} \\ =\sqrt[]{4+4} \\ =\sqrt[]{8} \end{gathered}`
`\begin{gathered} DA=\sqrt[]{(-1-2)^2+(0-0)^2} \\ =\sqrt[]{3^2} \\ =3 \end{gathered}`

Here, the opposite sides are congruent but adjacent sides are NOT.

It cannot be a square NOR can it be a rhombus because all of the sides are NOT the same .

So, the options C and A are eliminated.

Find the slopes:

`\begin{gathered} AB=(2-0)/(1-(-1)) \\ =(2)/(2) \\ =1 \end{gathered}`

`\begin{gathered} BC=(2-2)/(4-1) \\ =(0)/(3) \\ =0 \end{gathered}`
`\begin{gathered} CD=(0-2)/(2-4) \\ =-(2)/(-2) \\ =1 \end{gathered}`
`\begin{gathered} DA=(0-0)/(-1-2) \\ =(0)/(-3) \\ =0 \end{gathered}`

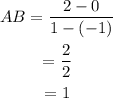
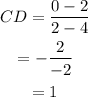
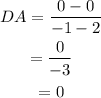
Parallel lines have equal slopes, so, the pair of sides AB and CD are parallel and the pair of sides BC and DA are parallel.

So, the adjacent sides are not perpendicular.

So, the quadrilateral cannot be a rectangle.

So, the correct option is B.