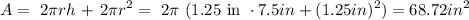For the cylinder to be able to contain the balls it has to have a radius equals to the radius of the ball, then the radius of the cylinder must be at least 1.25 inches. The height of the cylinder is 3 times the 'height' of each sphere, which is equal to the diameter of the sphere, the diamenter of a sphere is 2 times its radius then the height of the cylinder is h=6r = 7.5 inches.
Finally we apply the formula for the surface area of a cylinder: