Question

The rate of change in the function y=x+4 is________ the rate of change of the function represented in the table.

A) greater than

B) less than

C) equal to

x/y
0/6
2/8
4/10
6/12

Answer 1

recall that the slope is the "average rate of change" of any function.


`\bf y=\stackrel{slope}{1}x+4\qquad \qquad \begin{array}{ccll} x&y\\ \text{\textemdash\textemdash\textemdash}&\text{\textemdash\textemdash\textemdash}\\ 0&6\\2&8\\4&10\\6&12 \end{array} \\\\\\ \textit{let's check what is the slope of the tabled function}\\ \textit{by using two points from it}`

Answer 2

Option C.

Explanation:

The slope intercept form of a line is

`y=mx+b` .... (1)

The given function is

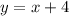`y=x+4` ..... (2)

On comparing (1) and (2) we get

`m=1`

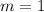
Rate of change of first function is 1.

If a line passes through two points
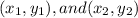`(x_1,y_1), and (x_2,y_2)`, the rate of change of the line is

`m=(y_2-y_1)/(x_2-x_1)`

From the given table it is clear that the line passes through two points (0,6) and (2,8). So, the rate of change of second function is

`m=(8-6)/(2-0)`

`m=(2)/(2)`

`m=1`

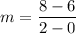
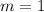
Rate of change of second function is 1.

The rate of change in the function y=x+4 is equal to the rate of change of the function represented in the table.

Therefore, the correct option is C.