Question

Given: A B C D is a rectangle.

Prove: The diagonals of A B C D are congruent.

The coordinates of rectangle ABCD are A(0, 0) , B(a, 0) , C(_,_), and D(0, b) .

The length of AC¯¯¯¯¯ is equal to ____.


The length of BD¯¯¯¯¯ is equal to ____.


The diagonals of the rectangle have the same length.

Therefore, AC¯¯¯¯¯ is congruent to BD¯¯¯¯¯.

Answer 1

Answer: Below is a screenshot of the test, the right answer confirmed. :)

Explanation:

Answer 2

The coordinates of C(a,b).

The length of AC diagonal is equal to
`√(a^2+b^2)`

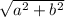
The length of BD diagonal is equal to
`√(a^2+b^2)`.

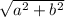Therefore, AC diagonal is congruent to BD diagonal.

Explanation:

Given

ABCD is a rectangle.

AB=CD and BC=AD

`m\angle A= m\angle B= m\angle C=m\angle D=90^(\circ)`

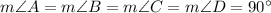
The coordinates of rectangle ABCD are A(0,0),B(a,0),C(a,b) and D(0,b).

Distance between two points
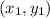`(x_1,y_1)` and
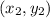`(x_2,y_2)` is given by the formula

=
`√((x-2-x_1)^2+(y_2-y_1)^2)`

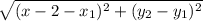
The distance between two points A (0,0) and C(a,b)

AC=
`√(( a-0)^2+(b-0)^2)`

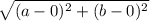
AC=
`√((a^2+b^2))`

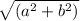
The length of AC diagonal is equal to
`√((a^2+b^2))`.

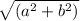Distance between the points B(a,0) and D(0,b)

BD=
`√((0-a)^2+(b-0)^2)`

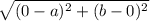
BD=
`√((a^2+b^2))`

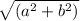
The length of BD diagonal is equal to
`√((a^2+b^2))`.

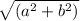The diagonals of the rectangle have the same length.

Therefore, AC diagonal is congruent to BD diagonal.

Hence proved.