Question

It took Gustavo 3 hours to drive to a football game. On the way home, he was able to increase his average speed by 20 mph and makethe return drive in only 2 hours. Find his average speed on the return drive.

Answer 1

Speed formula

`s=(d)/(t)`

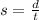
where

• s: speed, in mph

,

• d: distance traveled, in miles

,

• t: time elapsed, in hours

In the first trip, s = s1 and t = t1 = 3 hours, that is,

`\begin{gathered} s_1=(d)/(t_1) \\ s_1=(d)/(3) \end{gathered}`

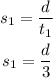
In the second trip, s = s2 and t = t2 = 2 hours, that is,

`\begin{gathered} s_2=(d)/(t_2) \\ s_2=(d)/(2) \end{gathered}`

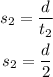
Notice that in the first and second trips the distance is the same, and that is why the same variable is used.

On the second trip, he was able to increase his average speed by 20 mph, then:

`s_2=s_1+20`

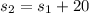
Substituting with the previous relationships:

`(d)/(2)=(d)/(3)+20`

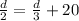
Solving for d:

`\begin{gathered} (d)/(2)-(d)/(3)=20 \\ (1)/(6)d=20 \\ d=20\cdot6 \\ d=120\text{ miles} \end{gathered}`

Substituting this result into the s2 formula:

`\begin{gathered} s_2=(120)/(2) \\ s_2=60\text{ mph} \end{gathered}`

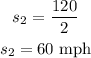
His average speed on the return drive was 60 mph