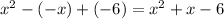Question

What is a quartic function whose only real zeros are the following x=-3 and x=2

Answer 1

y=
`x^(4)`+
`x^(3)`-
`5x^(2)`+x-6

Answer 2

x^2+x-6[/tex]

Explanation:

We have been given two zeroes x= -3 and x=2 of some quadratic equation

We have to find the quadratic equation when x=-3 is a zero means (x+3) is a factor and when x=2 is a zero means (x-2) is a factor

We have a formula to find the quadratic equation from zeroes is

`x^2-(sum of zeroes )x+product of zeroes`

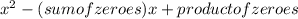
Here sum of zero is -3+2=-1

And product of zero is (-3)(2)=-6

substituting the values in the formula we will get

`x^2 -(-x)+(-6)=x^2+x-6`