Question

Jamila runs a grocery store that sells coffee beans blend by the pound.she wishes to mix 40 pounds of coffee to sell for a total cost of $222. to obtain the mixture she will mix coffee that sells for $5.10 per pound with coffee that sells for $6.30 per pound. how many pounds of each coffee should she use.

Answer 1

Let the $5.10 coffee be represented by x, and the $6.30 coffee be represented by y.

If she wishes to mix 40 pounds, this can be expressed as

`x+y=40\text{ ----------(1)}`

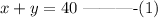
The total cost of both coffee is $222; this can be expressed as

`5.1x+6.3y=222\text{ -----------(2)}`

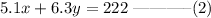
This provides a system of equations that can be solved simultaneously:

From equation 1, we can rewrite the equation to be

`x=40-y\text{ ----------(3)}`

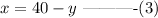
Substitute equation 3 into equation 2:

`5.1(40-y)+6.3y=222`

Solving, we have

`\begin{gathered} 204-5.1y+6.3y=222 \\ -5.1y+6.3y=222-204 \\ 1.2y=18 \\ y=15 \end{gathered}`

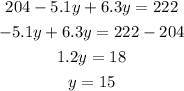
To solve for x, substitute y = 15 into equation 3:

`\begin{gathered} x=40-15 \\ x=25 \end{gathered}`

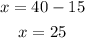
Therefore, Jamila needs 25 pounds of the $5.10 coffee and 15 pounds of the $6.30 coffee.