Question

Sergio, Kim, Sarah, lan, Larry, Maria, and Katrina have all been invited to a dinner party. They arrive randomly and each person arrives at a different time.a. In how many ways can they arrive?b. In how many ways can Sergio arrive first and Katrina last?c. Find the probability that Sergio will arrive first and Katrina last.

Answer 1

Part a

So we have 7 different people that arrive at a dinner party at different times and we must find how many possible combinations can happen. Let's assume that nobody has arrived yet. There are 7 possible people that can arrive first. Now let's assume the first person arrived, it doesn't matter who. Now there are 6 possible people that can arrive in second place. If we continue to make the same deduction you'll notice that from the first person to the seventh we have 7, 6, 5, 4, 3, 2 and 1 possible people that can arrive in that position. The total amount of combinations is given by the product of all these numbers:

`7\cdot6\cdot5\cdot4\cdot3\cdot2\cdot1=7!=5040`

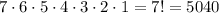
So they can arrive in 5040 different ways.

Part b

This one is similar to part a but with the difference that now we know that the first person is Sergio and the last is Katrina. This basically means that we must find all the possible combinations of the remaining 5 people. If we proceed like in part a this leads us to:

`5!=5\cdot4\cdot3\cdot2\cdot1=120`

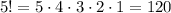
Then there are 120 different ways where Sergio arrives first and Katrina arrives last.

Part c

Now we have to find the probability that Sergio and Katrina arrive in the given order. This probability is given by the quotient between two numbers:

- The number of ways the 7 people can arrive if Sergio is 1st and Katrina 7th.

- The total number of ways the 7 people can arrive.

These two quantities are the ones calculated in part b and a respectively. Then the probability we are looking for in this part is given by:

`(120)/(5040)=(1)/(42)`

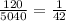
Then the probability that Sergio will arrive first and Katrina last is 1/42.