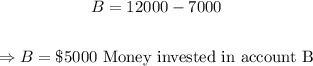Let us say that A and B represent the money invested in accounts A and B, respectively.
Then, if Mary invested $12 000 in total:
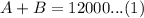
The formula for the simple interest is given by the equation:

Where r is the annual rate of interest and t is the time (in years).
From the problem, we identify:
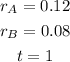
Then, the interests at the end of 1 year for each account are:
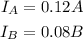
If the total interest is $1240:
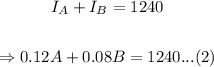
From (1):
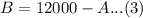
Using (3) in (2):

Finally, using this result on (3):