Question

g=10m/s2A brick with a mass of 3 kg is set on an incline angled at 37°. The block accelerates down the incline at 3 m/s2. What is the magnitude of the frictional force acting on the brick? (N)

Answer 1

We are given an object sliding down an incline with a friction force. A free-body diagram of the system is the following:

Now we will add the forces in the x-direction:

`\Sigma F_x=ma_x`

We will consider the forces that are in the direction of the movement as positive and the ones in the direction against the movement as negative. Plugging in the forces:

`mg_x-F_f=ma_x`

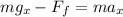
Now we solve for the friction force:

`-F_f=ma_x-mg_x`

Multiplying both sides by -1:

`F_f=mg_x-ma_x`

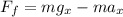
Now we determine the x-component of the weight using the following triangle:

From the triangle we can use the function cosine as follows:

`\sin 37=(mg_x)/(mg)`

From this we can solve for the x-component of the weight by multiplying both sides by "mg":

`mg\sin 37=mg_x`

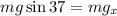
Now we use this expression and replace it in the sum of forces:

`F_f=mg\sin 37-ma_x`

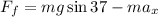
Now we plug in the known values:

`F_f=(3kg)(10(m)/(s^2))\sin 37-(3kg)(3(m)/(s^2))`

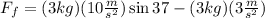
Solving the operations:

`F_f=171.5N`

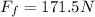
Therefore, the friction force is 171.5 Newtons.