ANSWER
-2.852i + 2.377 j
Step-by-step explanation
We have to find the projection of u onto v,
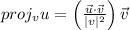
The vectors are:
• u = <-9, -5>
,
• v = <-6, 5>
Let's find the dot product,
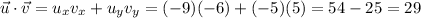
Now, find the modulus of v squared,
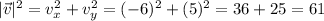
Now, we have to divide 29 by 61 and multiply each of the components of vector v by this constant,

Hence, the projection is the vector <-2.852, 2.377> or, using another notation, -2.852i + 2.377 j.