Question

Triangle 1:A(6,6),B(12,9),C(9,6) Triangle 2: A(2,2)B(4,3)C(3,2) what transformation was performed on triangle 1 to get the triangle 2? What scale factor was used to transform triangle 1 to triangle 2?

Answer 1

If we draw both triangles, we get the following:

notice that the transformation on triangle 1 made it smaller, then, we have a dilation.

To find the scale factor, we have to remember the general rule for the dilations on the cartesian plane:

`\begin{gathered} d_k(x,y)=(kx,ky) \\ k\\e0 \end{gathered}`

in this case, we can take the point A' on triangle 2 and the point A on triangle 1 , assuming that the transformation gave us the point on triangle 2:

`\begin{gathered} d_k(6,6)=(2,2) \\ \Rightarrow(6k,6k)=(2,2) \\ \Rightarrow6k=2 \end{gathered}`

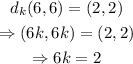
solving for k, we get:

`\begin{gathered} 6k=2 \\ \Rightarrow k=(2)/(6)=(1)/(3) \\ k=(1)/(3) \end{gathered}`

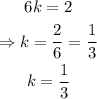
therefore, the scale factor is k = 1/3