The ordered pairs are (1,4), (5,6) and (7,7) of the form (n,g)
The rate of change is the slope of the equation
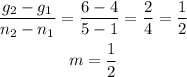
The equation of the linear function now becomes;
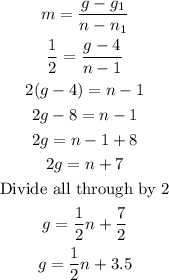
Hence the equation of the linear function is g = 0.5n + 3.5
Another equation for a function that has twice the rate of change and the same initial value becomes;
initial rate of change is 0.5
hence for this, the rate of change is 0.5 x 2
m = 1
the initial value is at n = 0,
so g = 0.5(0) + 3.5
g = 3.5
The new equation then becomes g = mn + C
g = 1n + 3.5
Hence the new equation that has twice the rate of change and the same initial value is g = n + 3.5