Question

A 175-g glider on a frictionless track is attached to a spring with a spring constant pf 155 N/m. It is moving at0.815 m/sand is 3cm from its equilibrium point. Use energy conservation to find:

Answer 1

Given:

The mass of the glider, m=175 g=0.175 kg

The spring constant of the spring, k=155 N/m

The speed of the glider, v=0.815 m/s

The distance of the glider from the equilibrium, x=3 cm

To find:

(a) Amplitude.

(b) Maximum speed.

(c) Angular frequency.

Step-by-step explanation:

(a)

The glider will have the maximum speed at the equilibrium point and minimum speed at the extreme points, that is the amplitude. Thus the kinetic energy of the glider will be maximum at the equilibrium point and will be minimum at extreme points.

The spring potential energy will be maximum at the extreme points and will be minimum at the equilibrium point.

From the law of conservation of energy, the energy of a system is constant. Thus the kinetic energy of the mass at equilibrium must be equal to the potential energy of the spring at the amplitude. If the mass is in between the equilibrium and extreme point, the energy will be equal to the sum of the kinetic energy of the glider and the potential energy of the spring.

Thus,

`(1)/(2)mv^2+(1)/(2)kx^2=(1)/(2)kA^2`

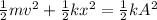
Where A is the amplitude.

On rearranging the above equation,

On substituting the known values,

`\begin{gathered} A=\sqrt{(\left(0.175*0.815^2+155*\left(3*10^(-2)\right)^2\right?)/(155)} \\ =0.041\text{ m} \end{gathered}`

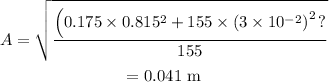
(b)

The maximum speed is given by,

`v_(max)=A\sqrt{(k)/(m)}`

On substituting the known values,

`\begin{gathered} v_(max)=0.041\sqrt{(155)/(0.175)} \\ =1.22\text{ m/s} \end{gathered}`

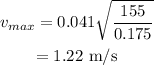
(c)

The angular frequency is given by,

`f=(1)/(2\pi)\sqrt{(k)/(m)}`

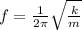
On substituting the known values,

`\begin{gathered} f=(1)/(2\pi)\sqrt{(155)/(0.175)} \\ =4.74\text{ Hz} \end{gathered}`

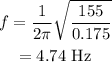
Final answer:

(a) The amplitude is 0.041 m

(b) The maximum speed is 1.22 m/s

(c) The angular frequency is 4.74 Hz