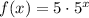Question

Please Help!!

The function f(x) = 5(1/5)^x is reflected over the y-axis. Which equations represent the reflected function? Check all that apply.


f(x) =1/5 (5)x
f(x) =1/5 (5)^–x
f(x) =1//5 (1/5)^x
f(x) = 5(1/5)^–x
f(x) = 5(5)^x
f(x) = 5(5)^–x

Answer 1

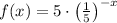Just the test, D and E are correct:

f(x)= 5(
`(1)/(5)`)
`^(-x)`

f(x)= 5(5)
`^(x)`

Answer 2

`f(x) = 5\cdot \left((1)/(5)\right)^(-x)` and
`f(x) = 5\cdot 5^(x)`

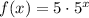
Explanation:

A reflected function means that each value of the original function can be obtained by using a value of x that has the same distance to the symmetry axis than original value of x. That is:

`y = f (L - x) = f (L + x)`

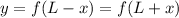
Since
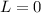`L = 0`, reflected function has the following form:

`f(-x) = 5\cdot \left((1)/(5)\right)^(-x) = 5 \cdot \left[\left((1)/(5) \right)^(x) \right]^(-1) = 5\cdot 5^(x) = 5^(1+x)`

Hence, correct options are:

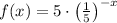`f(x) = 5\cdot \left((1)/(5)\right)^(-x)` and
`f(x) = 5\cdot 5^(x)`